- 本博客翻译自huggingface blog。
- 文末有惊喜
前言
基于Transformer的模型已经被证明了在许多NLP任务中的价值,但这类模型的时间复杂度、内存使用复杂度都是$n^2$(n为序列长度),因此当序列长度超过常规的512时,模型对算力的要求将会大幅提高。最近的一些文章Longformer, Performer, Reformer, Clustered attention都试图通过近似全主力机制改善该问题。例如这个帖子就是介绍这些模型的。BigBird论文是处理这类问题最新模型的其中之一,它使用block sparse attention替换了原类似Bert一样的全注意力机制,在与BERT一样的计算力情况下,可以处理的序列长度达到4096。它已经在很多长文本序列的任务上达到SOTA效果,例如长文本摘要、长文本问答。
BigBird RoBERTa模型现在已经可以在Transformers仓库中使用。这篇博客的目的是为了让读者深入理解big bird的运行机制,快速使用Transformers仓库上手BigBird模型。但在开始之前,我们需要知道,BigBird的注意力机制是一个近似BERT的全注意力机制,因此它不是说比BERT的注意力机制效果更好,而是运行效率更高。BERT的注意力机制的存储与序列长度是二次方关系,在长文本情况下的存储需求就已经开始令人难以忍受,而BigBird的block sparse attention就是为了解决这个问题。也就是说,在$\infty$长度序列上,计算$&\ \infty$次时,我们应该把BERT的全注意力机制换成block sparse attention。
如果你想知道,为什么在计算长序列时,我们需要更多的算力,这篇博客正好适合你。
当使用标准BERT一样的注意力机制时,主要的问题可能有:
- 每个词与其他所有词都有关系吗?
- 为什么每个词的注意力不仅仅集中在对它来说最重要的词
- 如何知道哪些词是重要的
- 如何有效的让注意力仅考虑个别一些词
在下面,我们来解答这几个问题
注意力应该考虑哪些词?
首先我们研究一个注意力工作的例子“BigBird is now available in HuggingFace for extractive question answering”。在全注意力机制中,每个词都会在注意力中计算其他所有词。用数学表达式表示即为:
$query-token\in{BigBird,is,now,available,in,HuggingFace,for,extractive,question,answering}$与$key-tokens=[BigBird,is,now,available,in,HuggingFace,for,extractive,question,answering]$全量计算注意力
让我们思考一下,如果通过掩码,让query-token只与最重要的key-token做注意力计算可能是一个更明智的方法,下面我们列举一下对query-token来说,重要的key-token都有哪些。
# 以下面句子为例
>>> example = ['BigBird', 'is', 'now', 'available', 'in', 'HuggingFace', 'for', 'extractive', 'question', 'answering']
# 现在query_token的例子为available
>>> query_token = 'available'
# 初始化一个空的key_token列表,下面我们逐渐添加
>>> key_tokens = []相邻的词是非常重要的,当前词的含义非常依赖于它邻近的前几个词和邻近的后几个词,这就是sliding attention
# 举例窗口为3,即只考虑available词的前一个词和后一个词
# 即左边的词”now“;右边的词”in“
>>> sliding_tokens = ["now", "available", "in"]
# 更新一下key_tokens集合
>>> key_tokens.append(sliding_tokens)长程依赖(Long-range dependencies):有的任务,需要捕获距离较远的词之间的关系,例如问答模型需要比较原文中每个词与整个问题,从而发现原文中哪些词序列更适合做正确答案。如果大多数原文词与其他原文词做注意力计算,而不是与问题做注意力计算,这对模型来说将会更困难的筛出重要的原文词。
BigBird有两种长程注意力方式,可以让计算变的更有效:
- 全局词(Global token):有一些词,需要考虑其他所有词,其他所有词也需要考虑它。例如”HuggingFace is building nice libraries for easy NLP“。如果”building“是一个全局词,模型在有的人物中需要知道词”NLP“和词”HuggingFace“的关系(这两个词在最左边和最右边),那么词”building“需要被设置成全局词,从而处理与”NLP“和”HuggingFace“的关系。
# 例如第一个词和最后一个词是全局的
>>> global_tokens = ["BigBird", "answering"]
# 将全局词加入至key_tokens集合中
>>> key_tokens.append(global_tokens)- 随机词(Random tokens):随机选择一些词,把信息传递给其他词,这可以降低词与词之间的信息交互难度。
# 现在用词”is“做随机词
>>> random_tokens = ["is"]
>>> key_tokens.append(random_tokens)
>>> key_tokens
{'now', 'is', 'in', 'answering', 'available', 'BigBird'}
# 现在,词”available“可以只与这些词做注意力计算,而不是所有词通过这种方法,query token只与部分词做注意力计算,同时与全注意力机制保持了相近的效果。这些操作会用于其他query_token,但是,所有这些操作都是为了在更节省的算力下,接近BERT的全注意力效果。在当今的硬件如GPU上,像BERT一样的模型,简单的将query token与所有的key token计算全注意力机制的方式,因为注意力时计算序列长度的平方矩阵乘法,所以非常消耗计算资源。然而如果通过结合sliding attention、global attention、random attention三种注意力机制,计算方式降为稀疏矩阵乘法,计算起来就更容易。BigBird就是通过block sparse注意力机制,结合了sliding attention、global attention、random attention三种方法。下面我们详细介绍
通过图结构理解global, sliding, random keys
首先,我们通过图来理解为什么三种注意力机制结合可以达到接近Bert的全注意力机制效果。
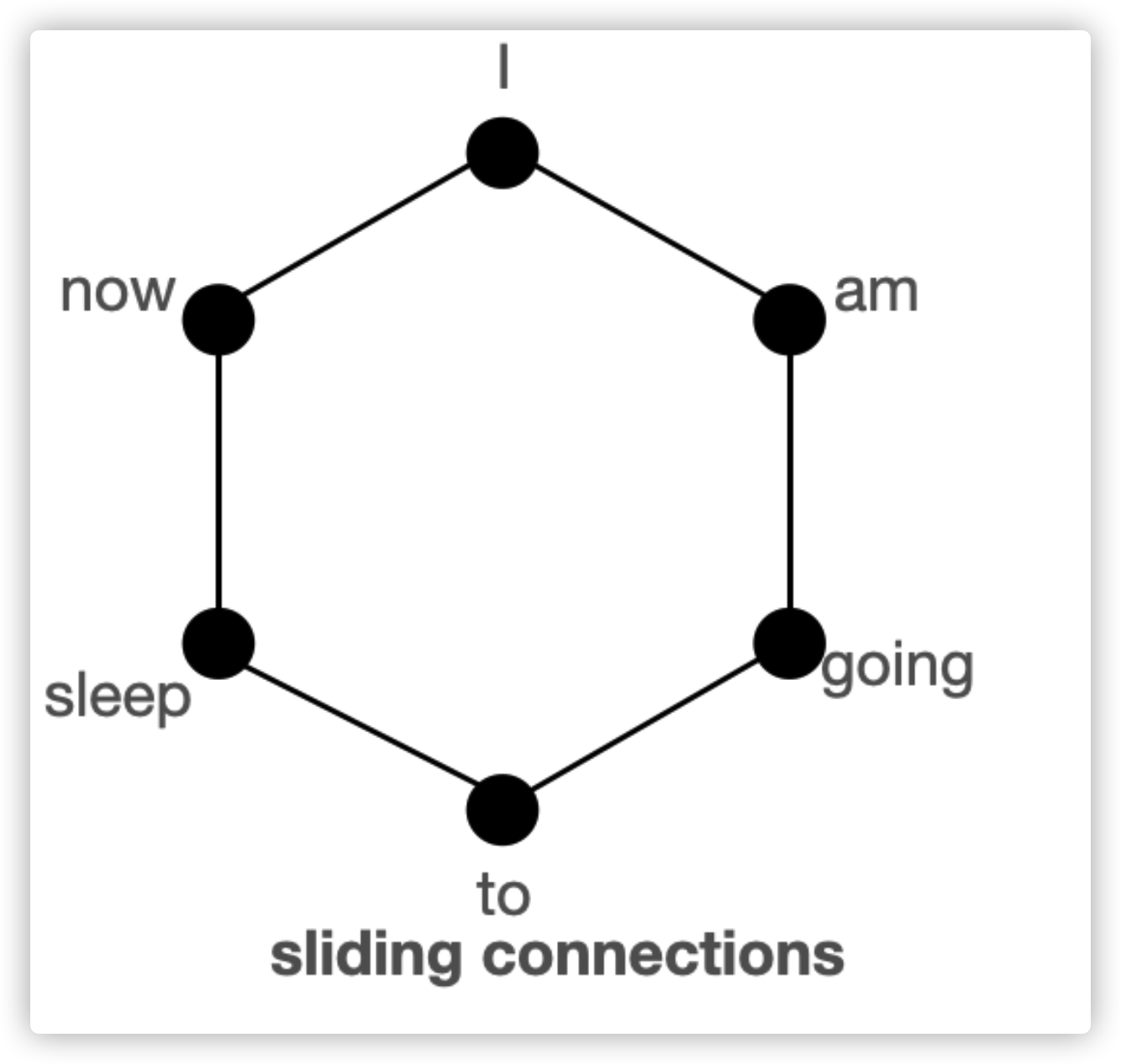
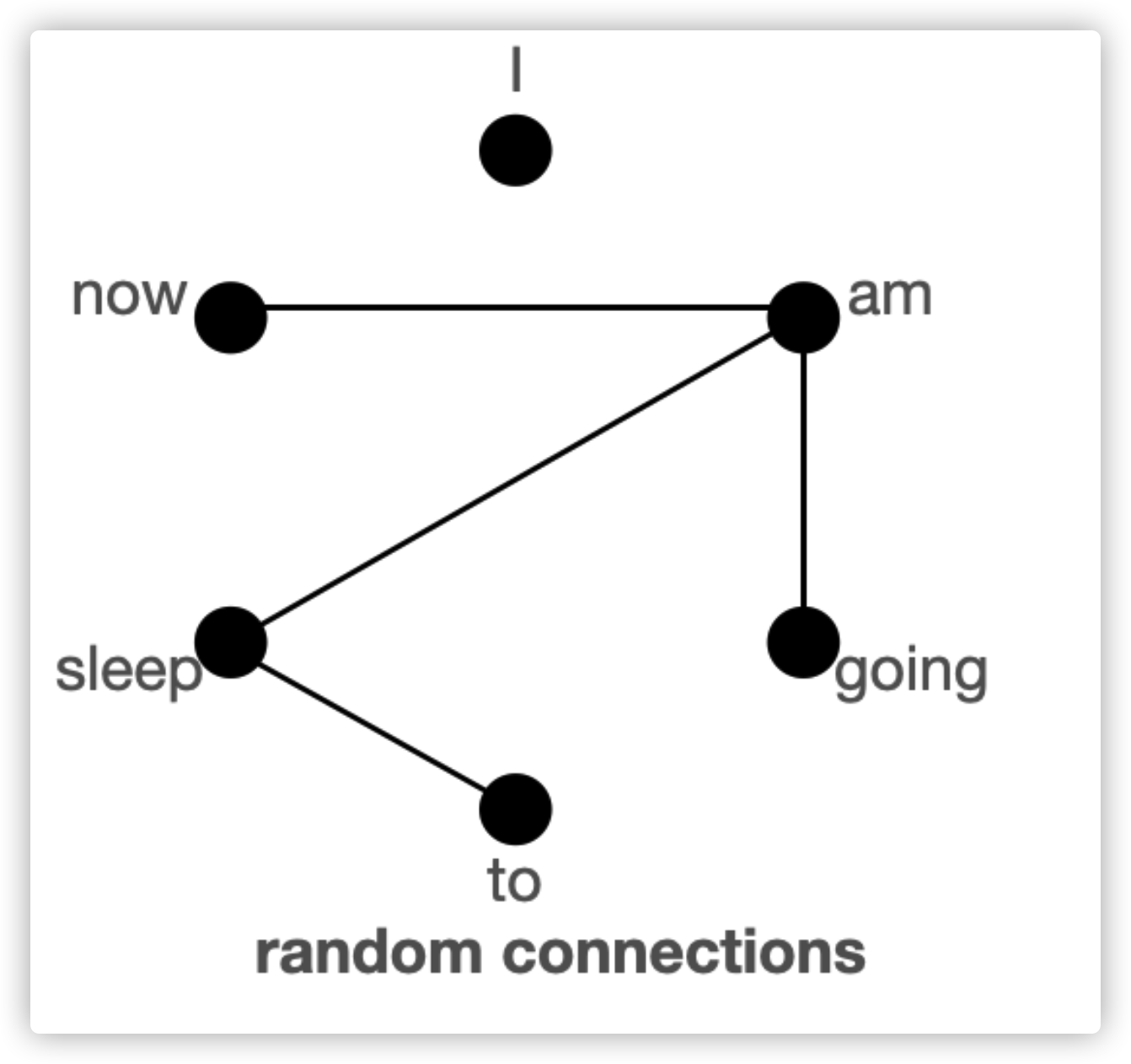
上图给出了global、sliding、random三种连接,每个节点代表了词,每条线代表了注意力,如果两个词之间没有连接,意味着两个词中间没有注意力计算。

BigBird block sparse attention结合了sliding、global、random的十条连接。正常注意力机制是有6个节点的所有15条连接。正常注意力与所有词都为全局注意力是等价的。
Normal attention:模型可以在一层之内,把每个词的信息都与其他任意词直接交互。以上图为例,如果模型需要两个词”going“与”now“互相联系,就需要在一层内,建立他们的直接连接。
Block sparse attention:由于节点不是全部互相连接的,那么模型的节点(或词)需要互相分享信息时,信息不得不通过最短路径的其他节点。例如,当“going”需要连接至“now”,如果只考虑窗口为左右各一个词的sliding attention,那么“going”与“now”之间的信息,必须通过going -> am -> i -> now,才能被“now”接收。因此,我们需要多层“Block sparse”才能有效捕获序列中所有的组合信息,而全连接的注意力机制只在一层内就可以捕获序列的所有组合信息。在极端情况下,如两个词距离最远,需要的层数,与输入的词数要一样多。当加入global connection的连接时,信息可以通过going -> i -> now的方式传递。如果加入random connections,信息可以通过going -> am -> now的方式传递。所以在有global connections、random connections的参与下,信息可以在token之间传递更有效。
如果当我们有很多global tokens时,就已经有很多足够短的连接了,那么就不再需要random connections。通过设置num_random_tokens = 0,就得到这样变体的BigBird模型,也称为ETC。
BigBird block sparese attention
通过以上讨论可知,Block sparse attention是一个有效的运行方式。每个词都是与其他global tokens、 sliding tokens、 random tokens进行计算,而不是与其他所有词进行计算。作者已经在代码中分别实现了多种注意力矩阵,因此实现了训练和预测时间更短的小技巧。
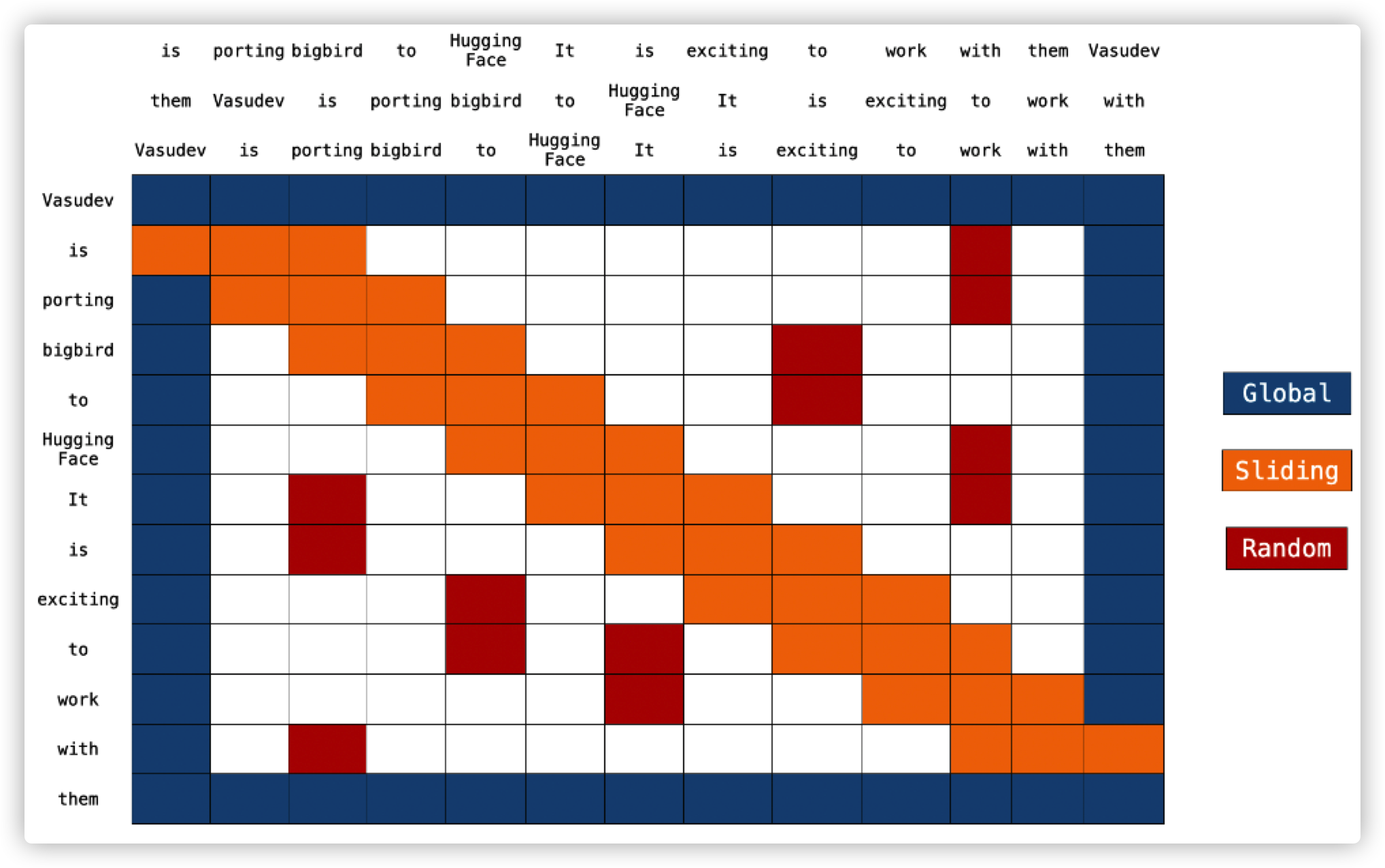
图中可以看到2个向左平移和向右平移的额外句子。这是计算sliding attention时需要执行的。
实现block_sparse注意力的代码看起来长,在这里会逐步解释。
Global Attention
对于global attention,注意力的每次query都是与输入的所有其他词进行计算。例如第一个词[Vasudev]和最后一个词[them]。如下代码所示
# pseudo code
Q -> Query martix (seq_length, head_dim)
K -> Key matrix (seq_length, head_dim)
# 1st & last token attends all other tokens
Q[0] x [K[0], K[1], K[2], ......, K[n-1]]
Q[n-1] x [K[0], K[1], K[2], ......, K[n-1]]
# 1st & last token getting attended by all other tokens
K[0] x [Q[0], Q[1], Q[2], ......, Q[n-1]]
K[n-1] x [Q[0], Q[1], Q[2], ......, Q[n-1]]Sliding Attention
计算注意力时序列中的key序列复制两次,一个向左平移一个位置、一个向右平移一个位置,然后用query序列与三个key序列直接向量相乘,就实现了所有sliding tokens的计算。计算复杂度仅为**O(3xn) = O(n)**。在上图中,橙色格子为sliding attention。在表格上方的三个句子代表三个key序列,即原key序列,向左平移的key序列、向右平移的key序列
# what we want to do
Q[i] x [K[i-1], K[i], K[i+1]] for i = 1:-1
# efficient implementation in code (assume dot product multiplication 👇)
[Q[0], Q[1], Q[2], ......, Q[n-1]] x [K[1], K[2], K[3], ......, K[n-1], K[0]]
[Q[0], Q[1], Q[2], ......, Q[n-1]] x [K[n-1], K[0], K[1], ......, K[n-2]]
[Q[0], Q[1], Q[2], ......, Q[n-1]] x [K[0], K[1], K[2], ......, K[n-1]]
# Each sequence is getting multiplied by only 3 sequences to keep `window_size = 3`.
# Some computations might be missing; this is just a rough idea.
Random Attention
Random attention可以在计算注意力时,让query词与其他随机的几个key词进行计算。在实际运行中,模型会随机收到几组注意力得分。
# r1, r2, r are some random indices; Note: r1, r2, r3 are different for each row 👇
Q[1] x [Q[r1], Q[r2], ......, Q[r]]
.
.
.
Q[n-2] x [Q[r1], Q[r2], ......, Q[r]]
# leaving 0th & (n-1)th token since they are already global模型推断
在一般的Bert注意力中,序列为$X=x_1, x_2,…,x_n$,由稠密向量$Q,K,V$计算的注意力为$Z=Softmax(QK^T)$。在BigBird注意力计算中,同样的算法就仅在个别的query向量和key向量之间计算。
下面我们来展开bigbird的block sparse attention的执行方式。首先我们假设b,r,s,g分别代表block_size, num_random_blocks, num_sliding_blocks, num_global_blocks。当b=4,r=1,g=2,s=3,d=5时:

注意力得分$q_1,q_2,q_3,q_{n-2},q_{n-1},q_n$分别由以下方式计算
注意力得分q1由$a_1$表示,第一个词与序列其他所有词计算得来$a_1=Softmax(q_1 * K^T)$
这里$q_1$代表第一个块,$g_i$代表第i个块,因此只是正常的注意力计算可得$q1\ &\ g$
在计算第二块时,需要前三块、最后一块、第五块,计算公式为$a_2=Softmax(q_2 * concat(k_1,k_2,k_3,k_5,k_7))$
图中的$g,r,s$代表global,random,sliding。
当计算注意力得分$q_{3:n-2}$时,需要用global, sliding, random三种key,与$q_{3:n-2}$进行注意力计算。这里的sliding key的计算由上面介绍的平移方法得到。
当计算倒数第二个词($q_{n-1}$)的得分时,需要第一个块、最后三块和第三块。计算公式为$a_{n-1}=Softmax(q_{n-1} * concat(k_1,k_3,k_5,k_6,k_7))$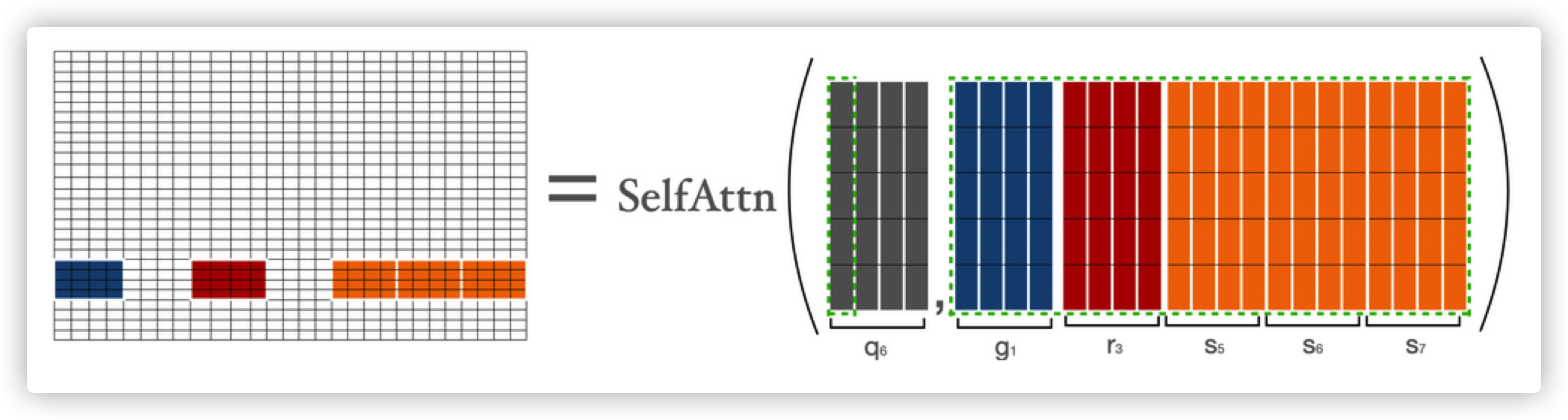
当计算最后一个词时,公式为$a_n=Softmax(q_n*K^T)$,这里的注意力计算为最后一个词与其他所有词的计算。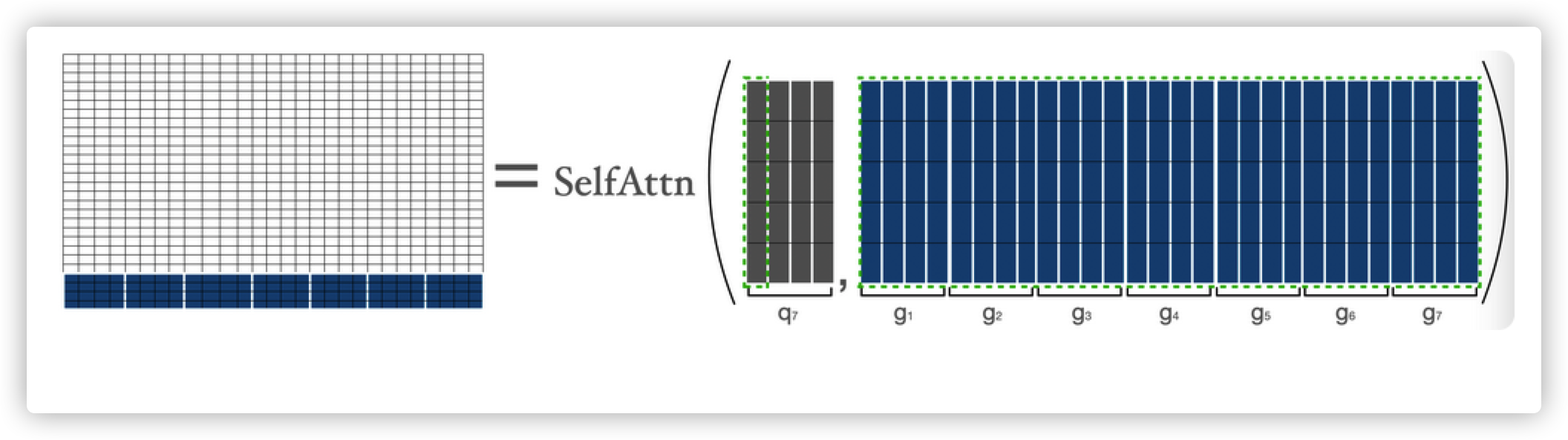
结合以上所有矩阵计算为: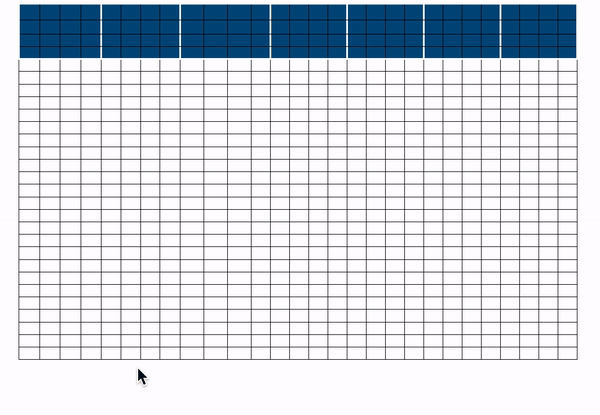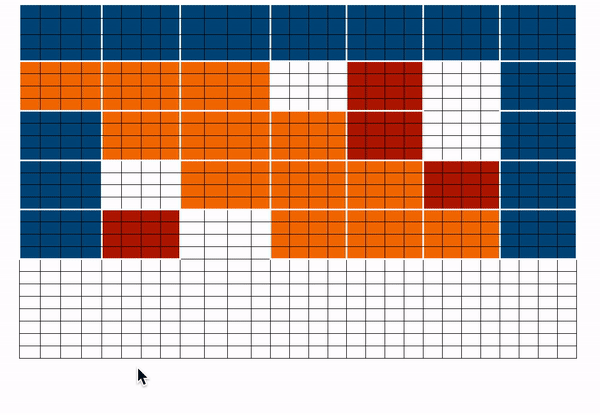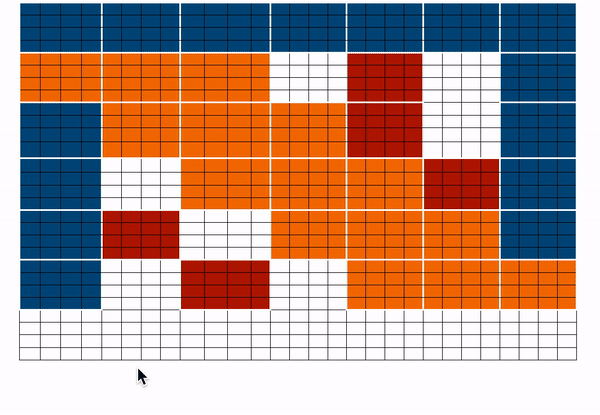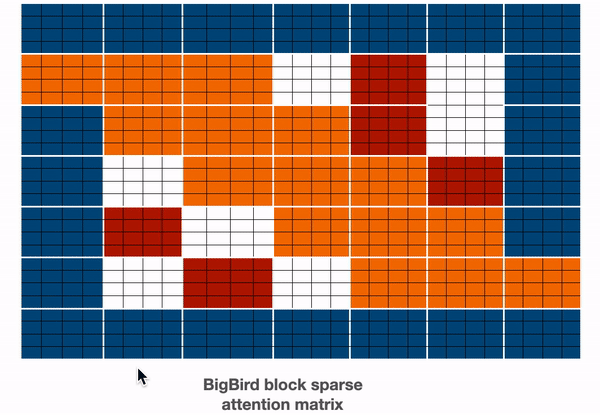
| 颜色 | 代表 |
|---|---|
| 蓝色 | global blocks |
| 红色 | random blocks |
| 橙色 | sliding blocks |
在神经网络前向传播时,因为矩阵中白色的块不会参与到注意力计算,所以计算整体会更轻量。
现在,我们已经看过了block sparse最难的部分了。希望你可以更好的理解block sparse的源码。
时间空间复杂度比较
| 注意力类型 | 序列长度 | 时间空间复杂度 |
|---|---|---|
| original_full | 512 | T |
| 1024 | 4×T | |
| 4096 | 64×T | |
| block_sparse | 1024 | 2×T |
| 4096 | 8×T |
- 计算过程
BigBird time complexity = O(w x n + r x n + g x n) BERT time complexity = O(n^2) Assumptions: w = 3 x 64 r = 3 x 64 g = 2 x 64 When seqlen = 512 => time complexity in BERT = 512^2 When seqlen = 1024 => time complexity in BERT = (2 x 512)^2 => time complexity in BERT = 4 x 512^2 => time complexity in BigBird = (8 x 64) x (2 x 512) => time complexity in BigBird = 2 x 512^2 When seqlen = 4096 => time complexity in BERT = (8 x 512)^2 => time complexity in BERT = 64 x 512^2 => compute in BigBird = (8 x 64) x (8 x 512) => compute in BigBird = 8 x (512 x 512) => time complexity in BigBird = 8 x 512^2
ITC vs ETC
BigBird模型可以由两种策略训练:ITC & ETC。ITC(internal transformer construction)即为上面讨论的计算方式。ETC(external transformer construction)为指定部分词为全注意力计算方式。
ITC需要更少计算量,因为只有很少的词是全局计算的,同时模型通过random attention保持全局信息。而ETC是设置了更多的全局计算词,面向一些需要一些额外的全局信息任务,例如在阅读理解任务中,问题需要与所有的答案进行注意力计算。
注意:在原论文中,ETC实验中,不含random token

夹带私货
现已开源中文bigbird预训练模型,从tiny至base共5个级别预训练模型。可以从huggingface hub直接下载使用,如果对您有用,欢迎star我的Github。



